Chemical bond between transition metal atom and hydrogen is important in surface chemistry and nanoparticle cluster catalysis, as the energetics of this bond breaking plays a critical role in hydrogen transfer process. The studies of Transition Metal (TM) systems present a challenge for theoretical description due to the presence of several electronic states close in energy which results in strong electron correlation. For this reason molecules containing TMs serve as an important testing ground for various methods in theoretical chemistry and molecular physics. Density functional theory (DFT) is the method of choice to study large systems, due to relatively low computational cost.
A clear advantage of unrestricted (also known as spin-polarized or broken spin-symmetry) solution is qualitatively correct description of band dissociation process. Since exact exchange-correlation functional is not known, unrestricted Kohn-Sham (UKS) treatment improves approximate functionals by taking part of the static electron correlation into account. The situation can be seen as localization of α and β electrons on the left and right atoms of the dissociating bonds, respectively (left-right electron correlation). Broken symmetry (BS) UKS thus describes the transition from closed shell system to biradical smoothly, which is not possible with restricted open shell KS (ROKS).
A disadvantage of UKS approach is that spin-polarized Slater determinant is no longer an eigenfunction of the spin operator. Hence, the average value of <Ŝ2> is not, generally equal to the correct value of Sz(Sz+1) (Here Sz is ½ of the difference in total numbers of α and β electrons). This situation is known as spin contamination and <Ŝ2> is often used as its measure. As a result of spin contamination, molecular geometry may be distorted toward the high-spin state one, spin density often becomes incorrect, and electron energy differs from the pure spin state ones.
Here we propose an alternative approach to variable spin-correction, based on canonical Natural Orbitals (NO). First, let us consider a two electron system such as stretched H2 molecule. We assume that restricted Kohn-Sham formalism yields higher energy for this system than unrestricted one, as the case of H2 molecule far from equilibrium. Unrestricted KS description produces the natural orbitals a, b as eigenvectors of the total density matrix with the orbital occupation numbers na, nb as corresponding eigenvalues. We further assume that na<nb which means that orbital a is antibonding, and orbital b is bonding NO. They are symmetry-adapted (a is σu and b is σg in case of H2 molecule). Corresponding spin-polarized broken symmetry orbitals p, q can be expressed as a linear combination of a and b using polarization parameter λ:
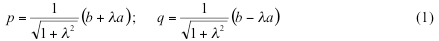
This parameter is determined by the occupation numbers na and nb as shown below. If alpha and beta electrons are localized on different parts of the molecule and do not overlap, the polarization parameter become unity and we arrive to Noodeman’s weak interaction limit. In the general case of many-electron system the orbitals of the alpha set, besides being orthogonal to each other, are also orthogonal to the orbitals of the beta set for a single exception of the corresponding beta orbital. The spin polarized orbitals obtained with the most standard quantum chemistry codes do not possess this property, which is why one has to produce the corresponding spin-polarized orbitals from NOs. BS solution can still be written as the Slater determinant in the basis of these corresponding orbitals as:
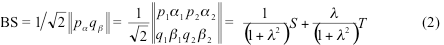
After some algebra, BS UKS energy can be written in terms of renormalized singlet and triplet state S0,T0 energies as:
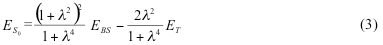
This energy includes the non-dynamic electron correlation effects arising from the mixing of
b1em>α1b2β2 and a1em>α1a2β2 states. In order to relate the polarization parameter λ to the occupation numbers na, nb, we can expand the electron density matrix in the basis of a and b orbitals and obtain.

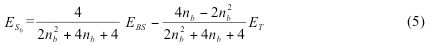
Thus, for a system with one correlated electron pair one can obtain the pure singlet energy expressed in terms of energy of BS UKS solution, the occupation number of the bonding NO, and the energy of the triplet built on these bonding and antibonding NOs (as opposed to self-consistant KS orbitals). This expression is applicable to two-electron systems as well as to the systems which have in addition the unpolarized electron core or ferromagnetically coupled unpaired electrons. Our approach is readily extended from spin contaminated systems with one correlated pair to multielectron systems. Spin-correction described above is implemented as a combination of unix shell script and FORTRAN code. It reads Natural Orbitals (NO) printout from Gaussian 03 job (keyword used was Punch=NO) and converts them into spin-polarized molecular orbitals according to eq (1). Script uses a threshold parameter to identify the correlated pair. The spin polarization of the electron core was neglected by adjusting the threshold value to consider natural occupations integer. The provision is made for the spin-up orbital p to be the one largely localized on metal atom and, so that spin-down orbital q is predominantly localized on H atom. The new alpha orbital set is made of doubly occupied NOs, orbital p, singly occupied NOs, and weekly occupied NOs. The new beta orbital set was identical, except that p was replaced with q. These orbitals were further used to evaluate the energy with single SCF step and verify that it is close to BS energy obtained at self-consistence. The energy of the triplet is calculated with another single SCF step using the original NOs only. It was used by the script to extract the energy of the pure singlet according to eq (3). The keywords used for single SCF step with the modified orbital set were SCF (MaxCycle=1) and Guess=Cards.
We apply it to study potential energy curves for 3d-TM hydrides. The equilibrium bond lengths and dissociation energies were found in good agreement with published ab initio results. Fermi smearing combined with wavefunction stability analysis was found necessary to obtain correct description.